let menu = ["Home", "Algorithms", "CodeHub", "VNOI Statistics"];

Overview

VOI 2013 MESSAGE1 - Trao đổi thông tin

solution.md

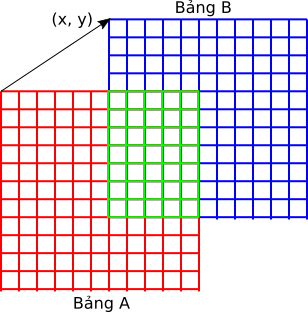
Ở bài này ta dời bảng B như hình, trong mỗi lần dời ta so sách các ô trong vùng giao nhau nữa 2 bảng, ô bằng nhau có giá trị 1, khác nhau có giá trị 0.

Cụ thể hơn, giả sử ta dời bảng B theo một vector \((x, y)\), khi đó ô \(A(i, j)\) sẽ được so sánh với ô \(B(i-x, j-y)\). Ta tính toạ độ các ô trong phần giao giữa 2 bảng như sau, có 4 điều kiện:

\[\begin{cases} 0 <= i < m\\ 0 <= j < n\\ 0 <= i-x < m\\ 0 <= i-y < n\\ \end{cases}\]

Từ đó suy ra:

\[\begin{cases} max(0, x) <= i < min(m, m + x)\\ max(0, y) <= j < min(n, n + y)\\ \end{cases}\]

Sau đó ta tìm hình chữ nhật chứa toàn số 1 và có diện tích lớn nhất (như bài QBRECT).

Sau đây là cách tìm hình chữ nhật như trên trong thời gian \(O(n^2)\):

Với mỗi ô \(j\) trên hàng \(i\), ta tìm \(f(j)\) là số ô 1 liên tiếp trên cột \(j\), tính từ hàng \(i\) trở lên. Sau đó, với mỗi cột \(j\), ta tiếp tục tìm ô gần nhất bên trái và ô gần nhất bên phải có \(f\) nhỏ hơn \(f(j)\), sau đó tính diện tích hình chữ nhật ở cột \(j\) là \(S = f(j)\times(r - l - 1)\) với \(l, r\) là chỉ số 2 ô bên trái và bên phải nói trên.

Hình minh hoạ khi tính \(f(4)\):

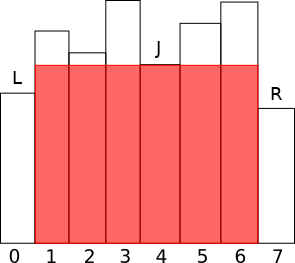
Để tìm \(l, r\) nhanh, ta dùng kĩ thuật sử dụng Deque tìm Min/Max trên đoạn tịnh tiến.

Độ phức tạp của toàn bộ lời giải là \(O(n^4)\).

main.cpp
Open in Github • Download 
#include <iostream>
#include <vector>
#include <string>
using namespace std;

void calc(int &res, int x, int y, const vector<string> &a, const vector<string> &b) {
    int m = a.size(), n = a[0].size();
    int low_i = max(0, x), high_i = min(m, m + x);
    int low_j = max(0, y), high_j = min(n, n + y);
    if ((high_i - low_i)*(high_j - low_j) <= res) return;
    vector<int> f(high_j, 0);
    vector<int> l(high_j), q(high_j), idx(high_j);
    for (int i=low_i; i < high_i; i++) {
        int top = 0;
        for (int j=low_j; j < high_j; j++) {
            if (a[i][j] == b[i-x][j-y]) {
                f[j]++;
                while (top && q[top-1]>=f[j]) top--;
                if (!top) l[j] = low_j-1;
                else l[j] = idx[top-1];
                q[top] = f[j], idx[top] = j, top++;
            } else {
                f[j] = 0;
                q[0] = 0, idx[0] = j, top = 1;
            }
        }
        top = 0;
        int r;
        for (int j=high_j-1; j >= low_j; j--) {
            if (f[j]) {
                while (top && q[top-1]>=f[j]) top--;
                if (!top) r = high_j;
                else r = idx[top-1];
                res = max(res, f[j]*(r - l[j] - 1));
                q[top] = f[j], idx[top] = j, top++;
            } else {
                q[0] = 0, idx[0] = j, top = 1;
            }
        }
    }
}

int main() {
    ios::sync_with_stdio(false); cin.tie(0);
    int T; cin >> T;
    while (T--) {
        int n, m; cin >> m >> n;
        vector<string> a(m), b(m);
        for (auto &s: a) cin >> s;
        for (auto &s: b) cin >> s;
        int res = 0;
        for (int i=-m+1; i<m; i++) for (int j=-n+1; j<n; j++) {
            calc(res, i, j, a, b);
        }
        cout << res << '\n';
    }
    return 0;
}
Comments