let menu = ["Home", "Algorithms", "CodeHub", "VNOI Statistics"];

Overview

VOI 2016 RBULL - Trại bò tót

solution.md

Tóm tắt:

Đầu tiên, tại mỗi ô ta tìm hình thoi có bán kính lớn nhất mà không có 2 ô có cọc trùng nhau. Sau đó tính tổng số cọc trong mỗi hình thoi tìm đuợc ở trên rồi lấy max để được kết quả. Phần 1 được làm bằng QHĐ, còn phần 2 ta xoay bảng lại 45 độ để tính số cọc. Sau đây là chi tiết lời giải.

Phần 1:

Chia hình thoi thành 4 tam giác vuông.

Tính \(F1[i][j]\) là chiều dài cạnh của tam giác vuông cân có đỉnh tại ô \((i,j)\) ,trong tam giác không có 2 ô có cọc kề nhau và có hướng như hình. Dĩ nhiên, tam giác đó phải lớn nhất có thể.

triangle

Để cho giống cách tính chu vi của hình thoi, ta trừ chiều dài cạnh cho 1.

Ta có:

  • \(F1[i][j] = min(F1[i-1][j], F1[i][j-1]) + 1\), khi trong 3 ô: \((i,j), (i-1, j), (i, j-1)\) không có 2 ô có cọc nào kề nhau.
  • Ngược lại, \(F1[i][j] = 0\).

Định nghĩa và tính tương tự với \(F2\), \(F3\) và \(F4\). Sau đó, tại ô \((i,j)\), bán kính hình thoi lớn nhất cần tìm là \(min(F1[i][j], F2[i][j], F3[i][j], F4[i][j])\).

Phần 2: Xoay bảng để đếm số cọc

Ta xoay bảng như sau:

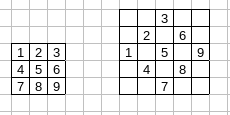
rotate

Công thức xoay bảng là \(F(i, j) = (1001 + i - j, 1 + i + j)\), tức là ô \((i,j)\) trong bảng ban đầu sẽ có tọa độ \((1001+i-j,1+i+j)\) trong bảng xoay.

Sau khi xoay, cần có cách tính số cọc trong hình thoi tâm \((i,j)\), bán kính \(r\).

Dễ thấy hình thoi sau khi xoay sẽ trở thành hình vuông, có đỉnh phải dưới tương ứng với đỉnh dưới của hình thoi ban đầu, và độ dài cạnh là \(2r+1\).

shape

main.cpp
Open in Github • Download 
#include <iostream>
#include <cstring>
using namespace std;

int __s[2017][2017];
int& s(int i, int j) {
    int ii = 1001 + i - j;
    int jj = 1 + i + j;
    return __s[ii][jj];
}
int sum(int i, int j, int d) {
    i += d;
    {
        int ii = 1001 + i - j;
        int jj = 1 + i + j;
        i = ii;
        j = jj;
    }
    d = d<<1 | 1;
    return __s[i][j] - __s[i-d][j] - __s[i][j-d] + __s[i-d][j-d];
}

bool a[1000][1000];
short f[1000][1000];
short g[1000][1000];

int main() {
    ios::sync_with_stdio(false); cin.tie(0);
    int m, n;
    cin >> m >> n;
    for (int i=0; i<m; i++) {
        string s;
        cin >> s;
        for (int j=0; j<n; j++) a[i][j] = s[j] == '*';
    }

#define rep(i,n) for (int i=1; i<n; i++)
#define rrep(i,n) for (int i=n-2; i>=0; i--)
    rep(i,m) rep(j,n) {
        if (!(a[i][j] && a[i-1][j]) && !(a[i][j] && a[i][j-1])) {
            f[i][j] = min(f[i][j-1], f[i-1][j]) + 1;
        }
        g[i][j] = f[i][j];
    }
    memset(f, 0, sizeof(f));
    rep(i,m) rrep(j,n) {
        if (!(a[i][j] && a[i-1][j]) && !(a[i][j] && a[i][j+1])) {
            f[i][j] = min(f[i-1][j], f[i][j+1]) + 1;
        }
        g[i][j] = min(g[i][j], f[i][j]);
    }
    memset(f, 0, sizeof(f));
    rrep(i,m) rep(j,n) {
        if (!(a[i][j] && a[i+1][j]) && !(a[i][j] && a[i][j-1])) {
            f[i][j] = min(f[i+1][j], f[i][j-1]) + 1;
        }
        g[i][j] = min(g[i][j], f[i][j]);
    }
    memset(f, 0, sizeof(f));
    rrep(i,m) rrep(j,n) {
        if (!(a[i][j] && a[i+1][j]) && !(a[i][j] && a[i][j+1])) {
            f[i][j] = min(f[i+1][j], f[i][j+1]) + 1;
        }
        g[i][j] = min(g[i][j], f[i][j]);
    }
    for (int i=0; i<m; i++) g[i][0] = g[i][n-1] = 0;
    for (int i=0; i<n; i++) g[0][i] = g[m-1][i] = 0;

    for (int i=0; i<m; i++) for (int j=0; j<n; j++) {
        s(i,j) = a[i][j];
    }

    for (int i=1; i<2017; i++) for (int j=1; j<2017; j++) {
        __s[i][j] += __s[i-1][j] + __s[i][j-1] - __s[i-1][j-1];
    }


    int res = 0;
    int ii, jj, gg;
    for (int i=0; i<m; i++) for (int j=0; j<n; j++) {
        int tmp = sum(i, j, g[i][j]);
        if (res < tmp) {
            res = tmp;
            ii = i;
            jj = j;
            gg = g[i][j];
        }
    }

    printf("%d %d %d %d", res, ii+1, jj+1, gg);

    return 0;
}
Comments