Fourier Transform 2 - Dãy Fourier với hệ số phức
Contents
Trong bài trước, dãy Fourier được định nghĩa hoàn toàn bằng số thực: \(g(t) = a_0 + \sum_{m=1}^{\infty}a_m\cos\frac{2\pi m t}{T} + \sum_{n=1}^{\infty}b_n\sin\frac{2\pi n t}{T}\\ a_0 = \frac{1}{T} \int_0^T f(t)\,\mathrm{d}t\\ a_m = \frac{2}{T} \int_0^T f(t)\cos\frac{2\pi m t}{T}\,\mathrm{d}t\\ b_n = \frac{2}{T} \int_0^T f(t)\sin\frac{2\pi n t}{T}\,\mathrm{d}t\)
Còn trong bài này ta sẽ định nghĩa dãy Fourier bằng số phức.
Giới thiệu sơ về số phức
Nếu bạn đã biết số phức, có thể bỏ qua phần này.
Dạng chuẩn
Mỗi số phức gồm phần thực và phần ảo: \(z = x + iy\). Với:
- \(x, y \in \mathbb{R}\) và \(i = \sqrt{-1}\).
- \(x\) được gọi là phần thực của \(z\): \(x = \mathrm{Re}[z]\).
- \(y\) được gọi là phần ảo của \(z\): \(x = \mathrm{Im}[z]\).
Như vậy, ta thấy mỗi số thực đều là số phức với phần ảo bằng 0.
Vài phép tính trên số phức
Phép cộng và phép nhân trên số phức được thực hiện bình thường:
\[z_0 = x_0 + iy_0, z_1 = x_1 + iy_1 \\ z_0 + z_1 = (x_0 + iy_0) + (x_1 + iy_1) = (x_0 + x_1) + i(y_0 + y_1) \\ z_0z_1 = (x_0 + iy_0)(x_1 + iy_1) \\ = x_0x_1 + ix_0y_1 + ix_1y_0 + i^2y_0y_1 \\ = (x_0x_1 - y_0y_1) + i(x_1y_0 + x_0y_1)\]Số phức liên hợp (complex conjugate) của \(z = x + iy\) kí hiệu là \(z^*\). Và có giá trị:
\[z^* = x - iy\]Module của số phức \(z\) là:
\[|z| = \sqrt{zz^*} = \sqrt{x^2 + y^2}\]Dạng lượng giác
Ngoài cách viết \(z = x + iy\), còn có một cách viết khác để biểu diễn số phức, gọi là dạng lượng giác của số phức.
Tuy nhiên, trước hết ta nhắc lại phương trình của Euler:
\[\mathrm{e}^{i\theta} = \cos\theta + i\sin\theta\]Như vậy, \(\mathrm{e}^{i\theta}\) là số phức với:
- Phần thực \(\mathrm{Re}[\mathrm{e}^{i\theta}] = \cos\theta\)
- Phần ảo \(\mathrm{Im}[\mathrm{e}^{i\theta}] = \sin\theta\)
- Module \(\vert \mathrm{e}^{i\theta}\vert = 1\)
Phép nhân và chia số phức dễ thực hiện hơn khi viết ở dạng lượng giác:
- \[d_1\mathrm{e}^{i\theta_1} \times d_2\mathrm{e}^{i\theta_1} = d_1 d_2 \mathrm{e}^{i(\theta_1 + \theta_2)}\]
- \[\frac{d_1\mathrm{e}^{i\theta_1}}{d_2\mathrm{e}^{i\theta_1}} = \frac{d_1}{d_2} \mathrm{e}^{i(\theta_1 - \theta_2)}\]
Fourier hệ số phức
Định nghĩa dãy Fourier đơn giản hơn rất nhiều:
\[g(t) = \sum_{n = -\infty}^{+\infty} \Large{c_n \mathrm{e}^{i\frac{2\pi n t}{T}}}\\ c_n = \frac{1}{T} \int_0^T \Large{f(t) \mathrm{e}^{-i\frac{2\pi n t}{T}}\mathrm{d}t}\]\(n\) là số nguyên, chạy từ âm vô cùng đến dương vô cùng.
Xét lại hàm \(f(t)\) với chu kì \(T = 2\) của bài trước:
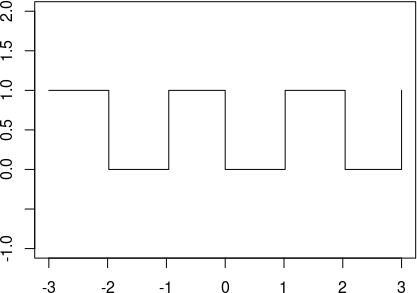
Nếu tính \(c_n\) theo công thức trên thì ta sẽ có:
- \(c_n = 0.5\) khi \(n = 0\)
- \(c_n = \frac{1}{i \pi n}\) khi \(n\) lẻ
- \(c_n = 0\) khi \(n\) chẵn, khác 0
Bạn đọc có thể dùng code này để chạy thử (ngôn ngữ R):
gsum = function(a, t) sum(sapply(a, function(n) 1/(1i*pi*n)*exp(1i*pi*n*t)))
g = function(n) function(t) 0.5 + gsum(0:n * 2 + 1, t) + gsum(-(0:n * 2 + 1), t)
x = -400:400 / 100
y = sapply(x, g(10))
plot(x, y, type='l')
Code trên gọi g(10) tức là ta dùng \(n\) từ -21 đến 21. n càng cao thì độ chính
xác càng cao.
Rất tiếc, vì R không hỗ trợ tính tích phân của hàm phức nên không có code tổng quát cho mọi hàm trong bài này.