let menu = ["Home", "Algorithms", "CodeHub", "VNOI Statistics"];

Duyệt đồ thị theo chiều sâu (DFS)

Duyệt đồ thị theo chiều sâu (DFS)

Contents

Duyệt đồ thị theo chiều sâu (DFS) là một thuật toán có nhiều ứng dụng trong tin học, đặt biệt là trong lý thuyết đồ thị. Một vài ứng dụng của DFS:

  • Tìm đường đi trên đồ thị
  • Tìm chu trình
  • Xác định thứ tự cha-con trên cây
  • Xác định các thành phần liên thông (TPLT)
  • Tìm TPLT mạnh
  • Tìm cầu, khớp
  • Tìm thành phần song liên thông
  • Sắp xếp topo
  • Quy hoạch động trên cây
  • Tìm LCA, truy vấn trên đường đi trên cây
  • Tạo mê cung ngẫu nhiên (Maze generation)
  • Kiểm tra tính phẳng của đồ thị (Planarity testing)

Và còn nhiều ứng dụng khác.

Thuật toán

DFS sẽ lần lượt ghé thăm các đỉnh của đồ thị một cách đệ quy. Các bước trong một lần ghé thăm đỉnh \(u\) được mô tả như sau:

  • Đánh dấu \(u\) đã được thăm
  • Duyệt trong các đỉnh \(v\) kề với \(u\):
    • Nếu \(v\) chưa được thăm, gọi đệ quy để ghé thăm \(v\)

Cài đặt thuật toán trong C++ như sau:

// Mảng để đánh dấu một đỉnh đã được thăm hay chưa
bool visited[N];

// Kiểu dữ liệu để lưu danh sách kề
typedef vector<vector<int>> dsk;

void dfs(int u, const dsk &ke) {
    // Đánh dấu đỉnh u đã được ghé thăm
    visited[u] = true;

    // Duyệt qua các đỉnh v kề với u
    for (int v: ke[u]) {
        // Nếu v chưa được thăm, gọi đệ quy dfs đỉnh v
        if (!visited[v]) dfs(v, ke);
    }
}

Với đồ thị vô hướng, mỗi lần duyệt DFS sẽ duyệt qua tất cả các đỉnh chung một thành phần liên thông.

Trang sau cho phép xem quá trình hoạt động của DFS: Depth-First Search Visualization

Một số điểm cần lưu ý

Phần sau xét DFS trên đồ thị vô hướng.

Sau khi chạy thuật toán, ta sẽ có được một cây từ đồ thị ban đầu. Cụ thể hơn, nếu đỉnh \(v\) được ghé thăm từ đỉnh \(u\) thì \(v\) sẽ là con của \(u\) trên cây.

Phần sau sẽ trình bày tính chất của cây được sinh ra bởi thuật toán DFS. Đây là cơ sở cho một số thuật toán sử dụng DFS như thuật toán tìm cầu và khớp.

Giả sử cây sau là kết quả của một đồ thị sau khi DFS:

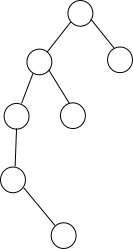
DFS result

Tất nhiên, đồ thị ban đầu còn nhiều cạnh khác nữa, tuy nhiên các cạnh đó đều phải là cạnh nối từ nút con lên nút tổ tiên. Ví dụ, các cạnh sau không thể tồn tại trong đồ thị ban đầu:

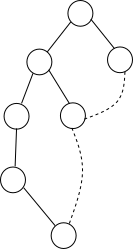
Invalid edges

Ví dụ một số cạnh hợp lệ:

Valid edges

Comments