let menu = ["Home", "Algorithms", "CodeHub", "VNOI Statistics"];

Thành phần song liên thông

Thành phần song liên thông

Contents

Bài này sẽ nói về thành phần song liên thông và cách tìm thành phần song liên thông.

Định nghĩa

Đỉnh khớp

Xét đồ thị vô hướng, đỉnh khớp (cut vertex) là đỉnh mà nếu xóa đi sẽ làm tăng số thành phần liên thông.

Ví dụ trong đồ thị sau, các đỉnh đỏ là đỉnh khớp:

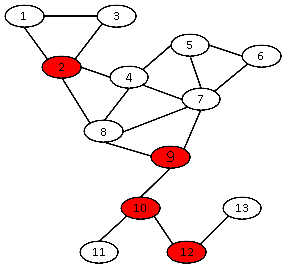
Cut vertex

Đồ thị song liên thông

Một đồ thị vô hướng được gọi là song liên thông (biconnected) nếu nó liên thông và không có đỉnh khớp, nghĩa là nếu xóa một đỉnh bất kì thì đồ thị vẫn liên thông.

Thành phần song liên thông

Xét đồ thị vô hướng \(G\), thành phần song liên thông được định nghĩa là đồ thị con song liên thông cực đại của \(G\). Cụ thể hơn, \(G'\) là một thành phần song liên thông của \(G\) thì ta có:

  • \(G'\) là đồ thị con của \(G\).
  • \(G'\) song liên thông.
  • \(G'\) là cực đại (maximal), nghĩa là không thể thêm đỉnh vào \(G'\) mà vẫn giữ được tính song liên thông.

Ví dụ trong hình sau, các đỉnh cùng màu cùng chung một thành phần song liên thông:

biconnected components

Ta thấy một đỉnh có thể thuộc vào nhiều thành phần song liên thông khác nhau và các đỉnh thuộc nhiều thành phần song liên thông đều là khớp.

Thuật toán tìm thành phần song liên thông

Có nhiều cách để tìm thành phần song liên thông, cách phổ biến nhất là duyệt theo kiểu Tarjan. Tuy nhiên, phần sau sẽ trình bày cách dùng phương pháp nén đường (path compression) và cấu trúc disjoint-sets để tìm thành phần song liên thông.

Ý tưởng

Ta thấy các đỉnh cùng nằm trên một chu trình đơn sẽ cùng thuộc một thành phần song liên thông.

Ý tưởng của phương pháp nén đường là kết hợp việc DFS với tìm TP song liên thông, các đỉnh cùng thuộc một TP song liên thông sẽ được hợp nhất lại bằng disjoint-sets.

dfs

Cụ thể, khi đang duyệt đỉnh \(u\) và có cạnh nối ngược lên \(v\), ta thấy các đỉnh \((v, 2, 3, u)\) tạo nên một thành phần song liên thông, ta sẽ hợp nhất các đỉnh này lại. Mỗi TP sau khi hợp nhất được đại diện bởi đỉnh có bậc nhỏ nhất trên cây DFS.

Tuy nhiên, do đỉnh \(v\) có thể thuộc TP song liên thông khác nên ta chỉ hợp nhất từ đỉnh \(2\) đến đỉnh \(u\).

Cài đặt

Trong quá trình DFS ta sẽ quản lý một stack chứa các đỉnh đang được duyệt, với các đỉnh đã được hợp nhất thì chỉ lưu đỉnh có bậc nhỏ nhất. Ngoài ra ta cũng cần lưu đỉnh con đang được duyệt của mỗi đỉnh.

Code như sau:

// Danh sách kề
typedef vector<vector<int>> dsk;

#define N 30001

// Cấu trúc disjoint-sets
int root[N];
int find(int u) {
    if (root[u] != u) root[u] = find(root[u]);
    return root[u];
}

bool visited[N];
int active[N];
vector<int> stack;

void dfs(int u, const dsk &ke) {
    visited[u] = true;
    root[u] = u;
    stack.push_back(u);

    for (int v: ke[u]) if (visited[v]) {
        v = find(active[v]);
        while (stack.back() != v) {
            root[find(stack.back())] = v;
            stack.pop_back();
        }
    }

    for (int v: ke[u]) if (!visited[v]) {
        active[u] = v;
        dfs(v, ke);
    }

    if (stack.back() == u) stack.pop_back();
}

Sau khi DFS xong, mỗi tập hợp trong disjoint-sets là một TP song liên thông, cộng thêm 1 đỉnh là đỉnh cha của gốc TP song liên thông đó.

Xem code giải bài SAFENET2 dùng đoạn code ở trên: /code/103.

Comments